控制方程
从概念模型到可进行一定机制判断和趋势预测的数学模型,需要依据概化的水文地质条件和污染物迁移转化特征,加入控制方程,边界条件,初始条件,含水层和隔水层的空间分布,外部应力(汇/源),以及孔隙介质和其中流体与污染物的物理化学特征,即将概念模型进行数学表达。进而,根据模型需要将场地的具体数据编制为输入文件,提供给计算程序进行计算,于是计算程序和输入文件一起构成具体场地的模型。概念模型的数学表达可以概括为以下几个方面:确定/选择控制方程,定义边界条件,定义初始条件,定义源/汇,以及选择参数(包括水文地质参数,溶质迁移参数以及化学反应参数)。溶质迁移控制方程与水流控制方程可以通过达西定律建立联系。
考虑对流-弥散过程的单一化学组分的三维溶质迁移控制方程:
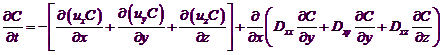
![]()
上式可以简写为:
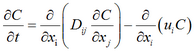
如果考虑汇源项、孔隙介质对溶质的吸附解吸作用和放射性衰变作用,则上式可写成一般形式:
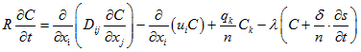
式中:R为阻滞因子,其值常大于1;n为 介质孔隙度,无量纲;C为 溶质的浓度,(ML-3);t为 时间,(T);Xij为在直角坐标系下沿各方向上的距离,(L);Dxx等为水动力弥散张量的9个分量,(L2T-1);u为 孔隙水流实际速度,(LM-1);qk为单位体积含水层给出或接受的流体的数量,代表源汇项,正值代表源,负值代表汇,(T-1);Ck是源汇项中溶质的浓度,(ML-3);δ是含水层的干容重,(ML-3);s是固体颗粒吸附的溶质浓度;λ是放射性元素蜕变(或生物降解)常数。
控制方程的解析解
控制方程是放之四海而皆准的客观规律,利用数学方法对地下水运动方程和溶质运移方程进行直接求解的计算方法叫做解析法。控制方程可能的解有无数组,必须存在额外的条件(即定解条件)方能给出针对具体问题的唯一解,这也是微分方程求解的基本特征之一。定解条件包括边界条件和初始条件(对非稳定流的情况)。从实用角度看,即使在数值方法相当发展后,解析解作为一种简单而实用的粗算手段,仍不失其重要价值。一般来说,可以首先利用解析解进行区域性拟合,倘若结果已经满意,则解析解即可作为最终结果,否则也可能启发人们去发现存在非均质或者存在越流等复杂条件,为进一步进行数值计算提供设计模型的依据,为模型校准提供好的初值和可能的变化范围。
控制方程的数值解
用离散化方法求解数学模型微分方程近似解的方法叫做数值法,数值解适用于各类复杂的解析解无法解决的水文地质条件。常用的数值模型的求解方法有有限差分法和有限元法。数值解模型可以更精确地体现地下水系统行为的各个方面,它能提供更强有力的工具表征和理解污染物迁移状况。同时数值模型具有相对较高的置信度,能够模拟随时间变化的地下水水流与污染物迁移情况。数值模型的构建需要定义合适的模拟区域,构建网格,选择合适的模拟软件来体现研究区域的水流以及污染物迁移特征,对比可靠的现场数据对模型进行校准以选择和调整合适的参数值,参考历史数据对模型进行验证,以及进行敏感性分析来分辨模型输入条件的敏感性。经过可靠校准的数值模型最终可用于合理预测污染物迁移扩散的时空趋势。建立和使用数值模拟需要有较高的相关教育背景的专业人员,对相应的资料、数据要求也较高。
边界条件
溶质迁移模型的边界条件也有三类:定浓度边界(Dirichlet条件),定浓度梯度或弥散通量(Neumann条件),以及定浓度和浓度梯度,或者说总通量(Cauchy条件)。溶质运移不但受边界条件的影响,还受支配它的水流和迁移边界条件共同作用,边界条件控制模型边界溶质的流入和流出。在实际应用中要注意结合水流方程的定流量边界,迁移方程的定浓度或定浓度梯度边界,综合考虑之后确定合适的迁移模型边界。溶质迁移模型边界条件的数学表达如下:
1)给定浓度边界(Dirichlet边界条件)
在边界上的浓度是已知的。若在边界B1上(x,y,z)点处t时刻的浓度值为f1(x,y,z),则第一类边界条件可表示为:
![]()
式中: B1 — 评估区D的第一类边界;f1(x,y,z,t) — B1上的已知函数。
2)给定弥散通量边界(Newman边界条件)
在边界上的弥散通量是已知的,即
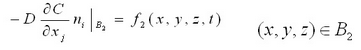
式中: f2(x,y,z,t) —已知函数;ni— 分别代表x,y,z方向上的外法线方向余弦。
3) 给定溶质通量边界(Cauchy边界条件)
在边界上的溶质通量是已知的,即
![]()
式中:f3(x,y,z,t) — 已知函数;vi — 分别代表经x,y,z方向的流速分量。
源/汇
源/汇表示水流或污染物进入或离开体系的机制。在溶质迁移控制方程中,源/汇项表示溶于水的溶质通过源进入或通过汇离开流场, 因此源/汇的描述可以用边界条件的表达式。源和汇大致分为内部和外部两类。外部源/汇实际上代表的是边界条件,如模拟中沿边界的指定水头,指定流量,以及水头变化的水流单元。内部源/汇指位于有效水流模拟区域内部的源和汇。例如井,掩埋式排水沟、补给、蒸腾,以及地表水体,如河、湖、池塘等。在三维或剖面模拟中,仅仅发生在地下水体系的上表面过程的源汇,例如补给,蒸腾,以及地表水体的渗漏,实际被看做边界条件。此外,其区别仅在于名称而不在于在模型中的表达。大多数计算程序中模拟编辑边界条件与内部源/汇的方法没差别。但是,有时某些过程作为溶质源处理,但它们并不是水流和迁移方程中所表示的水力源。例如进入含水层的NAPL缓慢溶解于研究区域的地下水中,此时存在溶质源,但没有水流加入系统。此时,可用加入一个或多个定浓度单元来表示,或者用一个溶解反应项来处理。
模拟前要指定内部源和潜在源点的浓度,这和处理边界单元是相同的。需要注意的是不同的源浓度处理方式不同,首先需要确定区域内所发生的物理,生物,和化学过程的特征。对于浓度随时间变化的源,注意区别不同浓度加载的函数。常见的浓度加载函数包括以下四种:1)脉冲载入(短期);2)连续源载入,浓度为常数(长期);3)连续源载入,浓度随时间变化(长期); 4)连续源载入,浓度衰减。
MODFLOW与MT3DMS耦合
MODFLOW是世界上使用最广泛的三维地下水水流模型。专门用于孔隙介质中地下水流动的三维有限差分数值模拟,由于其程序结构的模块化、离散方法的简单化及求解方法的多样化等优点,已被广泛用来模拟井流、溪流、河流、排泄、蒸发和补给对非均质和复杂边界条件的水流系统的影响。
MT3DMS是一套基于有限差分方法的污染物运移模拟软件,用于模拟地下水中单项溶解组分对流、弥散和化学反应的三维溶质运移模型,近年来在国外水文地质和水环境模拟等领域的研究中已经得到较为广泛的认可。MT3DMS不仅比较全面地考虑了污染物在地下水中的对流、弥散和化学反应等过程,而且可以灵活处理各种复杂的源汇项和边界条件,能够准确模拟承压、无压和越流含水层中的污染物运移过程。MT3DMS具有模块化的程序结构,允许独立或者联合进行运移组分模拟。
模拟计算时,MT3DMS需和MODFLOW一起使用。目前MT3DMS与地下水流模型MODFLOW已实现无缝连接,支持MODFLOW所有的水文和离散特性(包括1988版、1996版、2000版和2005版),已经广泛用于研究项目和野外模拟实例中。MT3DMS具有求解物质运移问题的独特套装选择,包括全隐式有限差分法(FDM),基于特征值质点追踪(MOC)及其变异方法,以及遵循质量守恒并能使数值弥散和人工振荡最小化的三阶总变量衰减法(TVD)。 MT3DMS用于求解三维对流、水力弥散、分子扩散、控制平衡或限制比率的吸附、以及一阶或零阶动力学反应。MT3DMS也可以采用双重介质质量运移公式求解受优先流影响的溶质运移。MT3DMS最近新增内容包括运移物观测(TOB)程序包,支持MODFLOW多结点井(MNW)和有回流的排水沟软件包,以及通过零阶动力学模拟地下水年龄的新功能。