Navigation:  溶质运移模型概化 > 22. 污染物迁移转化过程 > 22.2 对流迁移

 

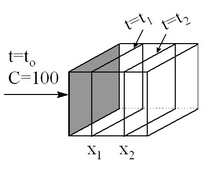
对流迁移

对流迁移是指溶解态污染物质在含水层中以地下水平均实际流速（即平均流速）迁移的现象。污染物的对流迁移过程取决于含水层性质，主要是渗透系数、有效孔隙度及水力梯度，与污染物本身属性无关。污染物在地下水中的对流迁移可用达西定律刻画。

式中：v—平均水流流速，（m/d）；K—渗透系数，（m/d）；i—水力梯度，(m)；n—孔隙度 ，(m/s)

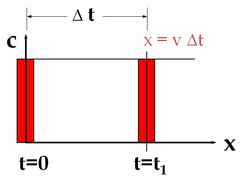
在对流迁移中，污染物浓度在运移过程中不发生损失，一般而言对流是溶质运移过程中的主控因素，渗透系数K是本过程的主要参数。

 

欧拉体系和拉格朗日体系

拉格朗日描述与欧拉描述乃描述流体运动的两种体系。拉格朗日描述取初始时刻（如时间t =0）流体质点的三维位置矢量R=(a,b,c)作为空间变量，并标记该流体质点。随着流体的运动，t 时刻的质点运动至新的三维空间位置r=(x,y,z)。显然，r与R具有函数关系：r  = r (R,t)，或用笛卡尔坐标分量表示为：

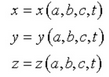
该关系其实给出了流体质点在空间的运动轨迹。由此可求出质点运动的速度——流速v，

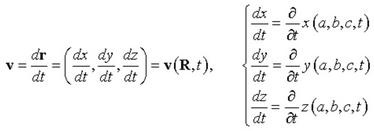
故流体的任何物理量不仅是时间t的函数，也是初始坐标矢量R的函数，此种以流体质点初始位置R和时间t描述流体运动的方法，即所谓的拉格朗日描述，其中R=(a, b, c)是拉格朗日坐标。其实，拉格朗日坐标相当于质点的“标签”。所以，拉格朗日描述记录了质点的时间演化，既可追溯质点的既往，也可预测质点的未来。

与拉格朗日描述不同，欧拉描述乃现实主义的描述手法。它仅关注“现在”——t 时刻处于空间r=(x,y,z)位置的质点。在此描述下，所有物理量皆表为空间位置坐标r（欧拉坐标）和时间t的函数。所以，欧拉描述所描绘的是流场在不同时刻的瞬时空间分布，其空间坐标r=(x,y,z)是纯数学的独立变量。

 

欧拉体系中的数值弥散

欧拉体系在固定的坐标系考察浓度场的运行。在此过程中，由于网格剖分不可能做到无限小，常常产生“数值弥散”，即在对流过程中产生的虚拟弥散，如下图所示。

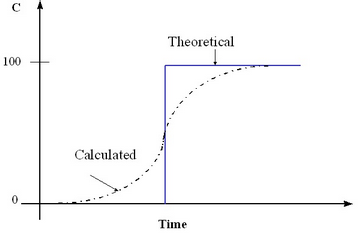
在数值弥散的作用下，即使不在地下水模型中考虑弥散，污染烟羽在运行中也会自发出现类似弥散的效果。通用的MT3DMS代码中包含了5种算法来解算对流-弥散方程：

●        显式差分：此方法使用了泰勒级数展开来近似导数，其计算过程会产生数值弥散。Zheng和Bennett（1996）的文章中指出，数值弥散度的        大小与网格大小的一半相当；

●        Method of Characteristics (MOC)：此算法中的数值弥散程度非常低，但计算量较大；

●        Modified Method of Characteristics (MMOC)：此算法降低了一些计算量，但浓度梯度较高的模型区域会产生明显的数值弥散；

●        Hybrid Method of Characteristics (HMOC)：此算法采用自动手段实现了MOC和MMOC的耦合；

●        Third-order total-variation-diminishing (TVD)：此算法使用高阶导数限制了数值弥散，但计算量远大于显式差分法。

应当指出的是，虽然数值弥散是被动出现的弥散，但其表观特征与真实在模型中指定的弥散度没有任何区别。在合适的情况下，如果模型工作人员对数值弥散的大小有把握，可以使用显式差分中的数值弥散代替场地中的实际弥散。

 

拉格朗日体系中的质点追踪

MODPATH 是一个用来计算质点追踪的程序，它与 MODFLOW耦合使用。 运行MODFLOW模拟之后，用户可以指定一系列质点的位置。使用计算所得的流场，模型可以追踪这些质点受对流作用影响的迁移过程。这些质点可以在时间上向前追踪，也可以向后追踪。质点追踪方法在划定水源井补给区的过程中尤其适用。一旦获取MODFLOW 流场后，要运行质点追踪只需要：1）创建质点的位置；2）指定模型网格的孔隙度信息。