Navigation:  水流模型构建 > 12. 地下水流概念模型的数学表达

 

控制方程

达西定律定义了水头差与流量之间的线性关系，可是单凭达西定律并不能真正描述地下水的流动，除非我们可以测量空间上每一点的水头，但这正是求解的目标。所以我们必须把地下水头这一物理量有效的限制起来，通常的做法是把地下水的水头通过含水层储水率这一系数转化成水量，而水量的变化即为流量，受达西定律的约束，这样就可以写出地下水流动的控制微分方程。根据概念模型的不同，控制方程的表现形式也不尽相同，影响因素有模型的维数（一维、二维、三维），水流状态（稳定流和非稳定流），介质状况（均质和非均质，各向同性和各向异性，孔隙，裂隙）等。下面列出了几种常见的水流控制方程，在具体工作中，应依据实际情况定义控制方程。

对于非均质、各向异性、空间三维结构、稳定地下水流系统的控制方程：

对于非均质、各向异性、空间三维结构、非稳定地下水流系统的控制方程：

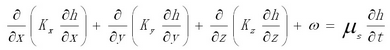
对于非均质、各向异性、空间三维结构、稳定地下水流系统的控制方程（适用于承压水）：

对于非均质、各向异性、空间三维结构、稳定地下水流系统的控制方程（适用于潜水）：

其中：h为水位，m；Kx，Ky，Kz—分别为x，y，z方向上的渗透系数，m/d；Tx，Ty，Tz分别为x，y，z方向上的导水系数，m2/d；t—时间，d；ω —源汇项，1/d；ε为源汇项，m/d；μs为贮水率，1/m。

 

不同维度模型的应用原则

 

控制方程的解析解

控制方程是放之四海而皆准的客观规律，方程中的水头和流量是循环指定的关系，可能的解有无数组，必须存在额外的条件（即定解条件）方能给出针对具体问题的唯一解（水头在空间上的分布情况），这也是微分方程求解的基本特征之一。定解条件包括边界条件和初始条件（对非稳定流的情况）。从某种意义上讲，定解条件中所包含的信息就是所研究的地下水系统的特征信息。在幸运的情况下，地下水工作者们能够把所研究区域的地下水系统特征概化总结成简单优美的定解条件；在更加幸运的情况下，他们可以使用这组定解条件推导出控制方程的解析解。

从实用角度看，即使在数值方法相当发展后，解析解作为一种简单而实用的粗算手段，仍不失其重要价值。一般来说，可以首先利用解析解进行区域性拟合，倘若结果已经满意，则解析解即可作为最终结果，否则也可能启发人们去发现存在非均质或者存在越流等复杂条件，为进一步进行数值计算提供设计模型的依据，为模型校准提供好的初值和可能的变化范围。

解析解需要对水文地质条件进行高度的简化，需要的参数在时空上是恒定的（如不能考虑渗透系数在水平方向和垂直方向的变化），这严重限制了解析解在实际问题中的应用。特别是以下情况：1.水力边界形状不规则；2.含水层的非均质性比较明显；3.多层含水层之间存在不均匀的越流；4.大降深的潜水问题。

 

控制方程的数值解

数值解适用于各类复杂的解析解无法解决的水文地质条件。常用的数值模型的求解方法有有限差分法和有限元法。数值解模型可以更精确地体现地下水系统行为的各个方面，它能提供更强有力的工具表征和理解污染物迁移状况。同时数值模型具有相对较高的置信度，能够模拟随时间变化的地下水水流与污染物迁移情况。数值模型的构建需要定义合适的模拟区域，构建网格，选择合适的模拟软件来体现研究区域的水流以及污染物迁移特征，对比可靠的现场数据对模型进行校准以选择和调整合适的参数值，参考历史数据对模型进行验证，以及进行敏感性分析来分辨模型输入条件的敏感性。经过可靠校准的数值模型最终可用于合理预测污染物迁移扩散的时空趋势。建立和使用数值模拟需要有较高的相关教育背景的专业人员，对相应的资料、数据要求也较高。

 

解析解和数值解的应用原则

 

各工作深度下数学模型选择