自然邻点法
自然邻点插值法广泛应用于一些研究领域中。其基本原理是对于一组泰森(Thiessen)多边形,当在数据集中加入一个新的数据点(目标)时,就会修改这些泰森多边形,而邻点的权重平均值将决定待插点的权重。
自然邻点插值的基本方程与反距离加权法插值中所用方程相同:
![]()
与反距离加权法插值相同,节点函数可以为固定值、梯度面或二次项函数。可以在自然邻点插值选项对话框中选择节点函数。不同之处在于权重的计算方法和选择用于插值的散点子集的方法。
自然邻点插值是基于散点集Thiessen多边形网的插值。可以对散点集用Delauney三角形化手段构建Thiessen多边形网。Delauney三角形化即使用Delauney标准构建TIN的过程。

每个散点在多边形网中对应一个Thiessen多边形,多边形内面积更接近于散点包围面积。散点集内部多边形为闭合多边形,位于凸面上的多边形为开放多边形。
对散点进行Delauney三角形化,形成的外接三角形就构成了Thiessen多边形,Thiessen多边形顶点即为相应三角形的图心。
局部坐标
自然邻点插值中的权重基于局部坐标概念,局部坐标将“和睦性”或其他散点产生的影响定义为插值点计算数值。此和睦性完全取决于周围散点的Thiessen多边形影响范围。
为定义插值点的局部坐标P n,需要知道多边形网中的所有Thiessen多边形的面积。临时在TIN中插入P n 会改变TIN和相应Thiessen网,会在P n 附近产生新的Thiessen多边形区域。
局部坐标的概念如下图所示,点1-10为散点,P n 为点1-10要插值的点,虚线表示未临时插入P n 点的Thiessen网边线,实线表示插入P n 后Thiessen网的边线。
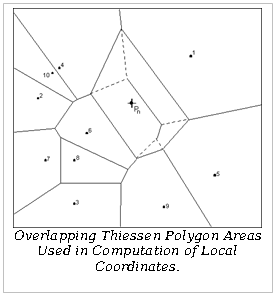
只有那些临时插入P n 时Thiessen多变形会发生改变的散点才会包含在散点子Thiessen集中被用来插值P n 点。因此上图中只有点1、4、5、6和9用于插值。这些与P n 相关的散点的局部坐标被定义为P n 点定义的的Thiessen多边形和未插入P n 点前每个点定义的Thiessen多边形的共享区域。相同的面积越大,生成的局部坐标越大,散点对于插值点P n 的影响和权重越大。
如果定义k(n) 为点P n 相应的Thiessen多边形面积,定义k m (n)为未插入P n和插入后相邻点P m 相应的Thiessen多边形面积的差异,局部坐标l m (n)函数如下所示:
![]()
插值方程中,局部坐标l m (n)在零、1和权重w m (n)间变化。如果正好P n 在P m的位置,则P n 和P m的Thiessen多边形面积相同,为1。一般情况下,P m 与P n 的相对距离越大,对其最终插值结果的影响越小。
外插值
如上图所示,TIN边界上的散点的Thiessen多边形为开放多边形。因为这些多边形有无限的面积,所以不能直接使用自然邻点插值,因此需要一种特别的方法来实现自然邻点法的外插值。插值前,插值到的特征对象(有限差分网格、有限元网格等)的X和Y边界是确定的,且在特征对象外部10%(此值可自行修改)处有显示对象范围的外边框。会在外边框的四个角创建四个临时的“假散点”,此时使用反距离加权法中的梯度面节点法来估算假散点的数值。此时在插值过程中,拥有外推值的假散点包含在了实际散点中。因此,保证了散点集凸面中所有的点都可以进行插值。当插值完成后,删除假散点。