克里金法
克里金插值法的名称来源于南非采矿工程师D. G. Krige,他创建这种方法用来精确的估计矿石储量。过去几十年中,克里金插法变为地质统计学中一个基础性工具。
克里金法基于被插值的参数可以被当做区域化变量的假设。区域化变量是处于完全随机变量和完全确定变量中间的变量,其以连续的方式从一个位置变化到另一个位置,点之间相近但在统计学上相互独立,且点与点之间有一定的空间关联性 (Davis, 1986)。克里金是一系列线性回归操作,用来将预设的协方差模型的估算方差最小化。
因为克里金法是一个比较复杂的插值方法,包含许多选项,如果使用者感兴趣,可以参看GSLIB教材获得更多信息:
Deutsch, C.V., & A.G. Journel. GSLIB: Geostatistical Software Library and User's Guide . Oxford University Press, New York, 1992.
其它有关克里金方法的教材包括:
Royle, A.G., F.L. Clausen, & P. Frederiksen. Practical Universal Kriging and Automatice contouring. Geo-Processing , Vol. 1, No. 4, 1981.
Davis, J.C. Statistics and Data Analysis in Geology . John Wiley & Sons, New York, 1986.
Lam, N.S. Spatial Interpolation Methods: A Review. The American Cartographer . Vol. 10, No. 2, 1983.
Heine, G.W., A Controlled Study of Some Two-Dimensional Interpolation Methods, COGS Computer Contributions , Vol. 2, No. 2.
Olea, T.A., Optimal Contour Mapping using Universal Kriging. J. Geophys. Research , Vol. 79, No. 5, 1974.
Journel, A.G., & Huijbregts, C.J. Mining Geostatistics . Academic Press, New York, NY, 1978.
常见的克里金算法包括:
普通克里金
在普通克里金算法中,第一步是从待插值的散点生成变差函数。一个变差函数由两部分组成:试验变差函数和模型变差函数。假定f是待插值的数据集,则试验变差函数为数据集中每一点针对所有其余点的方差(g),将方差与点距(h)作图可见如下所示。
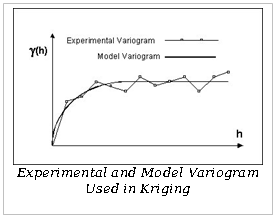
试验变差函数计算完成后,需要定义模型变差函数。模拟变差函数是一个用来模拟试验变差函数的简单数学方程。模拟变差函数随后被用来计算克里金算法中的权重。一般而言,克里金算法可以产生最好的局部最优线性无偏估计。所谓线性是指估计值是样本值的线性组合,即加权线性平均,无偏是指理论上估计值的平均值等于实际样本值的平均值,即估计的平均误差为0,最优是指估计的误差方差最小。
简单克里金
简单克里金是普通克里金的变种,它使用全局均值,而普通克里金方法使用局部均值。简单克里金不如普通克里金方法精确,但一般而言会产生更为平滑的差值结果。
泛克里金
按照空间场是否存在偏移可将克里金插值分为普通克里金和泛克里金。克里金算法的前提是散点空间分布较为均匀,即空间各处的局部平均值变化不大。当这一前提不成立时(例如一个斜坡),数据集就出现了所谓偏移。对于这种情况,可以暂时引入一个偏移项来保证局部均匀得到满足。