Clough-Tocher法 |
  
|
Clough-Tocher法 |
|
Clough-Tocher法
Clough-Tocher插值常在有限元方法的文献中出现，因为其源于数值分析的有限元方法。在插值前，散点先三角形化形成临时TIN。对每个三角形定义了一个二次多项式，由一系列三角Clough-Tocher面组成一个插值面。
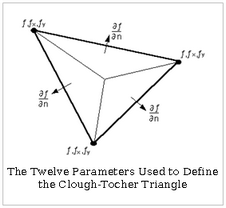
Clough-Tocher式是由12个参数定义的三次多项式，参数如上图所示：函数值f，每个顶点的一阶导数 f x 和 f y ，和三角形三边中点的法向导数 (Clough & Tocher, 1965; Lancaster & Salkauskas, 1986)。顶点一阶导数可以用周围三角形的斜率平均值来估算。单个基元被三角形图心和顶点的连接线分成了三个子基元。
如下所示的完整三次多项式被创建：
针对每个子三角形都会创建此三次多项式，这能保证跨越三角形连接线和边界的斜率连续性，但二阶导数的连续性不能被保证。
因为Clough-Tocher法是一个局部插值方法，其具有速度优势，很大的散点集也可以快速插值完毕。同时，该插值方法可以准确表达数据集局部趋势，创建平滑的插值面。
因为TIN只能覆盖散点集凸面，所以使用Clough-Tocher法无法进行超出凸面的外插值。其他散点集凸面外的点，在进行外插时被设置为默认数值，该数值可在插值选项对话框底部输入。