线性插值法 |
  
|
线性插值法 |
|
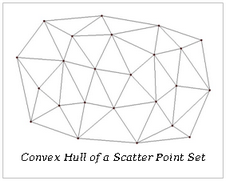
线性插值法
线性插值法与手工绘制等值线相近，这种方法是通过在数据点之间连线以建立起若干个三角形来工作的。所有连接得到的三角形的边都不能与另外的三角形相交，其结果构成了一张覆盖数据点范围的，由三角形拼接起来的网。 每一个三角形定义了一个覆盖该三角形内数据点的面。三角形的倾斜和标高由定义这个三角形的三个原始数据点确定。给定三角形内的全部结点都要受到该三角形的表面的限制。
如果选中线性插值方案，2D散点会首先三角化构成一个临时TIN。TIN将散点用三角网相连，用来将散点插值到其他特征对象，如有限差分网格或有限元网格。
利用三角形三个顶点定义平面，其所用方程如下所示：
其中A、B、C和D通过三个顶点的坐标值 (x1,y1,z1)、(x2,y2,z2)和 (x3,y3,z3)计算所得：
平面方程还可写成：
上式为计算三角形任一顶点高程的平面方程。
因为TIN只能覆盖散点集凸面，对凸面外部区域不能使用线性插值法进行外插值。其他散点集凸面外的点，在进行外插时被设置为默认数值，该数值可在插值时进行设定。下图所示为2D散点集被插值到2D有限差分网格，
