散点->均匀网格（克里金） |
  
|
散点->均匀网格（克里金） |
|
散点 > 散点>均匀网格（克里金）
克里金插值
克里金插值法的名称来源于南非采矿工程师D. G. Krige，他创建这种方法用来精确的估计矿石储量。过去几十年中，克里金插法变为地质统计学中一个基础性工具。
克里金法基于被插值的参数可以被当做区域化变量的假设。区域化变量是处于完全随机变量和完全确定变量中间的变量，其以连续的方式从一个位置变化到另一个位置，点之间相近但在统计学上相互独立，且点与点之间有一定的空间关联性 (Davis, 1986)。克里金是一系列线性回归操作，用来将预设的协方差模型的估算方差最小化。
ENVIFUSION中运用的克里金方程基于Deutsch and Journel (1992)发表的地统计学软件图形库(GSLIB)方程。因为克里金法是一个比较复杂的插值方法，包含许多选项，完全描述克里金法不是本手册的主要内容，所以如果使用者感兴趣，可以参看GSLIB教材获得更多信息：
Deutsch, C.V., & A.G. Journel. GSLIB: Geostatistical Software Library and User's Guide . Oxford University Press, New York, 1992.
其它有关克里金方法的教材包括：
Royle, A.G., F.L. Clausen, & P. Frederiksen. Practical Universal Kriging and Automatice contouring. Geo-Processing , Vol. 1, No. 4, 1981.
Davis, J.C. Statistics and Data Analysis in Geology . John Wiley & Sons, New York, 1986.
Lam, N.S. Spatial Interpolation Methods: A Review. The American Cartographer . Vol. 10, No. 2, 1983.
Heine, G.W., A Controlled Study of Some Two-Dimensional Interpolation Methods, COGS Computer Contributions , Vol. 2, No. 2.
Olea, T.A., Optimal Contour Mapping using Universal Kriging. J. Geophys. Research , Vol. 79, No. 5, 1974.
Journel, A.G., & Huijbregts, C.J. Mining Geostatistics . Academic Press, New York, NY, 1978.
在普通克里金算法中，第一步是从待差值的散点生成变差函数。一个变差函数由两部分组成：试验变差函数和模型变差函数。假定f是待插值的数据集，则试验变差函数为数据集中每一点针对所有其余点的方差（g），将方差与点距（h）作图可见如下所示。
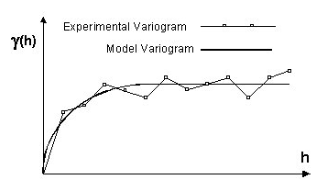
试验变差函数计算完成后，需要定义模型变差函数。模拟变差函数是一个用来模拟试验变差函数的简单数学方程。模拟变差函数随后被用来计算克里金算法中的权重。一般而言，克里金算法可以产生最好的局部最优线性无偏估计。所谓线性是指估计值是样本值的线性组合，即加权线性平均，无偏是指理论上估计值的平均值等于实际样本值的平均值，即估计的平均误差为0，最优是指估计的误差方差最小。
简单克里金是普通克里金的变种，它使用全局均值，而普通克里金方法使用局部均值。简单克里金不如普通克里金方法精确，但一般而言会产生更为平滑的差值结果。
散点>均匀网格（克里金）
本工具从空间离散的散点数据出发，按照用户指定维度生成均匀网格，并根据高斯正态分布算法为每个网格赋值。
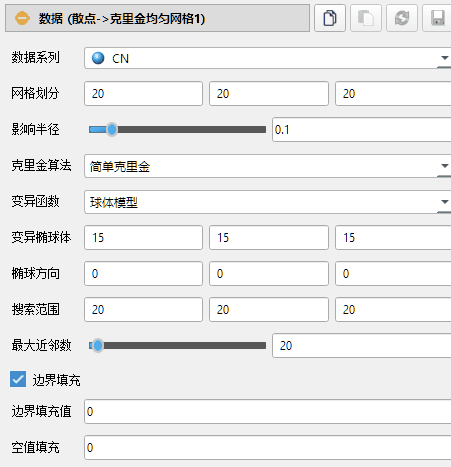
数据系列：请选择插值需要使用的数据系列。
网格划分：请在三个方向指定网格划分精度。
影响半径：请指定对散点原生空间的外扩比例，默认为0.1，即在各个方向外扩百分之十。
克里金算法：EnviFusion支持简单克里金和普通克里金。
变异函数：请在球体模型、指数模型和高斯模型中选择。
变异椭球体：当进行差值时，只有被插值点一定范围内的散点数据会被使用，而这一范围可以由此椭圆划定。默认情况下，搜索空间是一个圆形（3D情况下是球体）。
椭球方向：请指定变异椭球体在三个方向的旋转角度。最小为0度，最大为180度。
搜索范围：请在三个方向指定网格搜索的范围。系统认定当前数据点的影响范围仅限于此范围之内。
最大近邻数：请指定克里金算法所指定的最大近邻数。
边界填充：对生成体积的空间边界使用指定值填充。
边界填充值：请指定填充值。
空值填充：对生成体积之外的空间使用固定值填充。
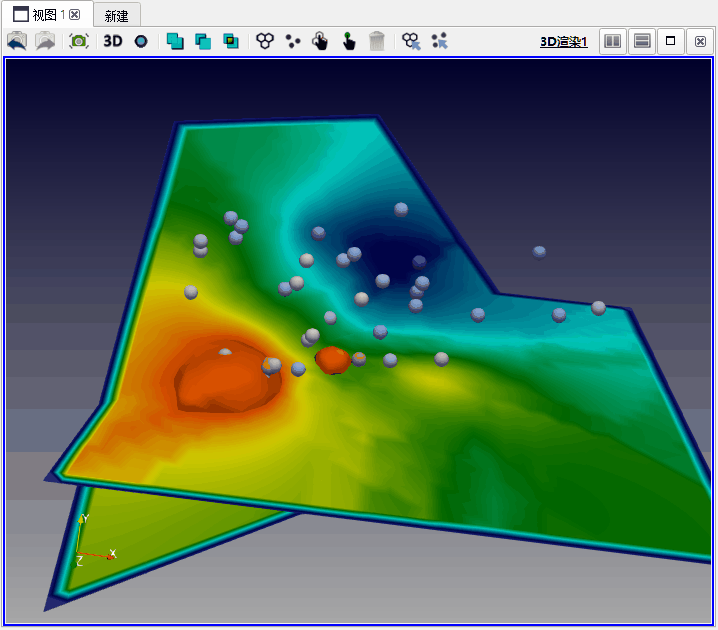
图示为克里金法生成的污染数据体及若干切片。