主成分分析 |
  
|
主成分分析 |
|
地球化学 > 主成分分析
主成分分析
使用主成分分析（PCA）算法对数据进行降维分析。主成分分析旨在利用降维的思想，把多指标转化为少数几个综合指标。主成分分析利用线性变换把输入向量变换到一个新的坐标系统中，使得数据投影的第一大方差在第一个维度（第一主成分）上，第二大方差在第二个维度（第二主成分）上，依次类推。主成分分析属于无监督学习，主要作用是减少数据集的维数，同时保持数据集的最大特征。EnviFusion支持对散点数据、网格数据、附加数据、表格数据等进行主成分分析。
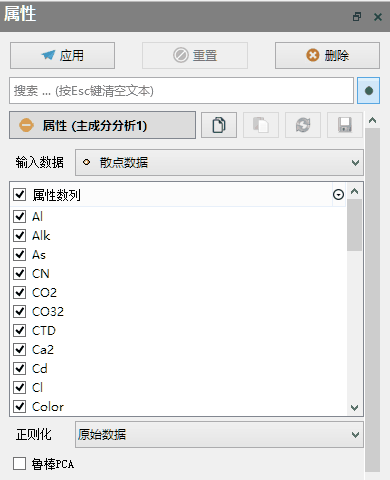
输入数据：请指定输入数据类型。包括散点数据、网格数据、附加数据、表格数据等。
属性数列：请选择参与计算的属性数列。
正则化：使用协方差矩阵对输入数据进行正则化可防止过拟合，避免大值属性控制模型走向，提高模型的泛化能力。但使用原始数据可以获得更好的收敛稳定性，用户可根据自身数据特点灵活选用。
鲁棒PCA：使用中值而非均值计算PCA，提高模型的鲁棒性。
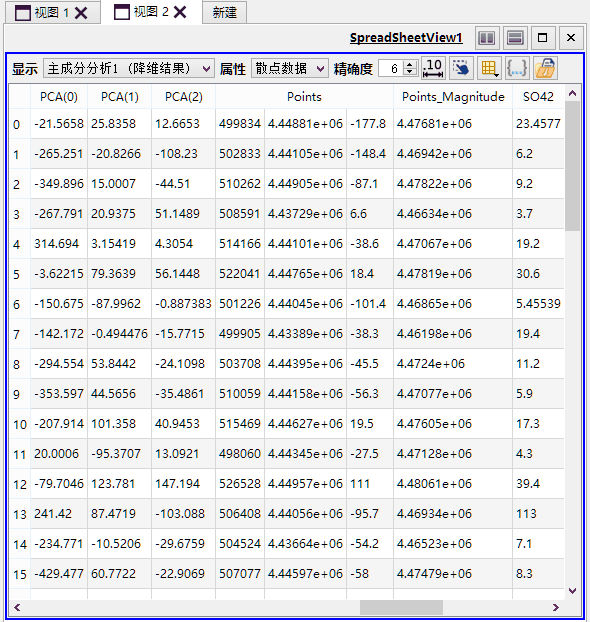
如上图所示，执行主成分分析后将在结果图层数据中生成三列新字段，分别为第一（PCA0）、第二（PCA1）、和第三（PCA2）主成分。可以理解为原始数据投影到新的三维空间后的散点坐标。