数据补齐 >时间序列补齐(SOM)
时间序列补齐(SOM)
在地下水监测领域,时间序列数据是必不可少的基础数据。传统的时序数据补齐通常以插值为基础,其中最为简单的插值方法为临点法,即以时间向前最靠近的或向后最靠近的有效数据作为该时间点的数据值;工程上运用较多的插值方法为样条插值,该方法需要插值所在位置前后两个或三个连续数据点,通过二次及三次多项式的拟合完成拟真。多项式插值的插值信息,根据多项式次数,仅来自临近的几个数据点,对于长时间序列的大范围补齐,有天生的缺陷。特别是面对周期数据时,无法捕捉周期涨落规律。本工具中使用的时间序列补齐方法应用了自组织神经网络 (SOM),对全时段的时间序列增量进行统一学习,并在此基础上对缺失的数据区段进行预测和补齐。
自组织图 (SOM) 或自组织特征图 (SOFM) 是一种无监督机器学习技术,用于生成高维数据集的低维(通常为二维)表示,同时保留数据集的拓扑结构。数据。例如,具有在 n 个观测值中测量的 p 个变量的数据集可以表示为具有相似变量值的观测值集群。这些集群然后可以被可视化为二维“地图”,这样近端集群中的观察值比远端集群中的观察值具有更多相似的值。这可以使高维数据更容易可视化和分析。SOM 是一种人工神经网络,但使用竞争学习进行训练,而不是其他人工神经网络使用的纠错学习(例如,反向传播和梯度下降)。 SOM 由芬兰教授 Teuvo Kohonen 在 1980 年代引入,因此有时被称为 Kohonen 地图或 Kohonen 网络。 Kohonen 地图或网络是一种计算方便的抽象,建立在 1970 年代的神经系统生物模型 和可追溯到 1950 年代 Alan Turing 的形态发生模型上。
属性补齐工具在填补缺失数据时也同样使用了SOM工具,但其中参加训练的是属性数据本身;而在本工具中,参与训练的是时间序列数据的时序差分值,所以预测是基于断点位置的属性值和空缺位置的差分值共同确定的,既照顾了数据序列的连续性,又综合考虑了时序变化特征。SOM模型是无监督训练模型,预测结果较为保守温和,适用于缺失时间较短和多井数据共同训练的场景。本工具在使用时将首先累积输入图层中所有时间点的属性数据,进行统一训练,随后进行补齐操作。
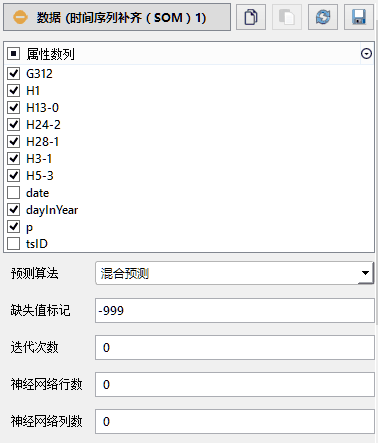
属性数列:请选择参与SOM训练的属性数列。SOM的学习优化过程并不在意维度之间的逻辑关系,非传统指标的加入也不会对聚类结果产生重大影响,这样就为数据探索过程赋予更大的自由度。
预测算法:请指定时间序列的预测算法。正序预测意味着时间序列将从前至后依次进行训练;逆序预测意味着时间序列将从后向前依次训练;系统默认的混合差分则将使用二者的平均值。
缺失值标记:请输入数据集中代表缺失值(NaN)的整型数字,默认为-999。在准备原始数据时,请将缺失的数据统一替换为此数值。
迭代次数:请指定神经网络训练的迭代次数,若为0系统将使用默认步数:20步。一般不需要用户干预。
神经网络行数:请指定神经网络的行数,供熟悉SOM的用户手工指定。如不指定,系统将自动计算。
神经网络列数:请指定神经网络的列数,供熟悉SOM的用户手工指定。如不指定,系统将自动计算。
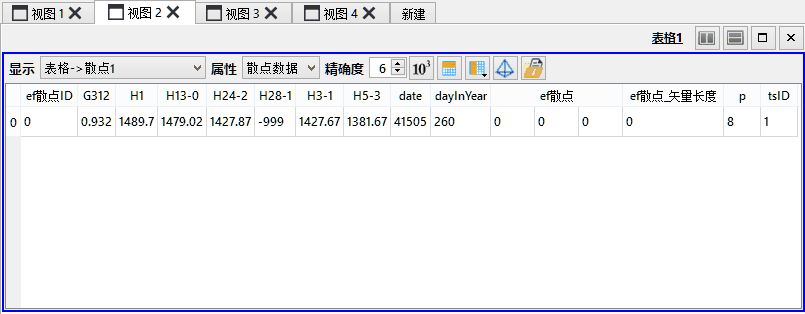
如上图所示,输入图层的散点数据中包含510个时间步,每一时间步中存在若干监测井的水位信息。运行本工具时,系统将首先收集全部时间段中的所有数据,并统一进行训练。
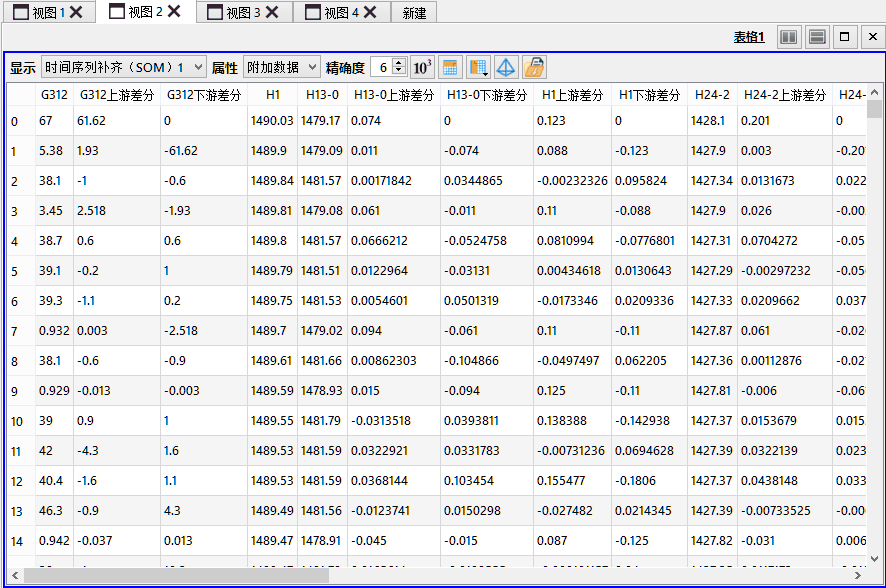
使用本工具后,输出图层的表格数据中将出现补齐之后的所有数据,注意原始数据中代表缺失数据的-999已经全部被替换成为SOM神经网络预测后的数值。其中带有“上游差分”和“下游差分”的数列为系统所预测的时序差分值。当原始数列存在缺失时,这些差分值会被用来进行数列的补齐。