散点->曲面（三角化） |
  
|
散点->曲面（三角化） |
|
散点 > 散点->曲面（三角化）
散点->曲面（三角化）
使用Delaunay二维算法从散点生成三角网格。Delaunay是实际中应用最多的三角剖分算法，以下是有关Delaunay的一些基本信息：
➢Delaunay边：E是点集中的点作为端点构成的封闭线段集合。假设E中的一条边e（两个端点为a,b），e若满足下列条件，则称之为Delaunay边：存在一个圆经过a,b两点，圆内(注意是圆内，圆上最多三点共圆)不含点集V中任何其他的点，这一特性又称空圆特性。
➢Delaunay三角剖分：如果点集V的一个三角剖分T只包含Delaunay边，那么该三角剖分称为Delaunay三角剖分。
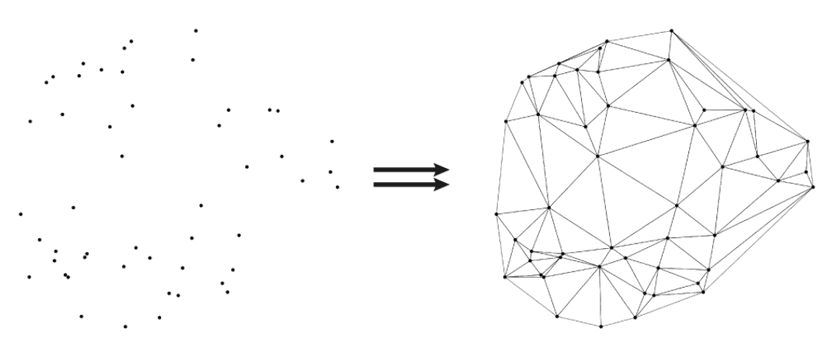
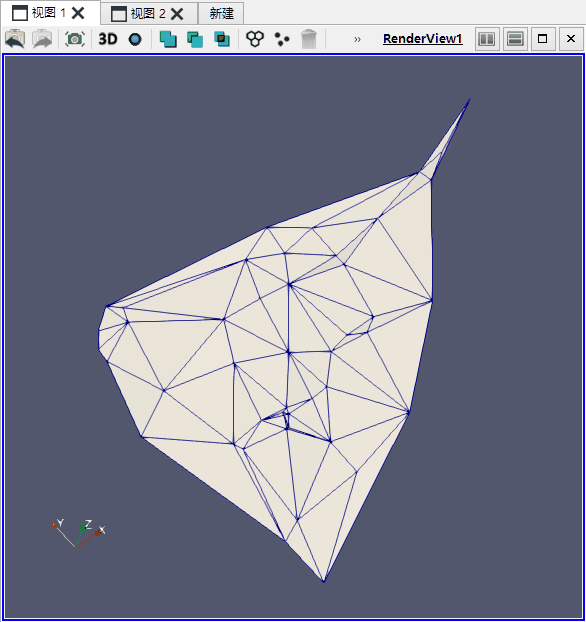
根据上述法则，可以将空间离散点连接成Delaunay三角形。
投影平面：本属性规定生成曲面时所选择的投影平面。包括XY平面和自动选择。一般环境地学领域数据可以选择XY平面，若数据最佳投影面不在XY平面，可尝试让系统自动选择最佳投影面。
重复点检验阈值：当两点过于接近时，距离低于此阈值的点将被合并为同一点。
初始偏移：当网格生成算法不稳定时，可以尝试将此参数适当调大。