Navigation:  III. 基础概念 > 图形渲染

 

基础概念>图形渲染>

渲染指生成三维场景或数据集的计算机图像，是计算机图形学的核心目标。

 

渲染方程

图形渲染由几个要素组成，分别为三维对象几何，一组光源，以及一个视角。从计算机处理角度，可以把这个过程描述为在给定数据集的每一个点上应用渲染方程。一般而言，渲染方程具有复杂的形式，描述了该点入射光、出射光、和材料特性之间的关系。由于需要考虑场景内不同点间的反射与散射关系，完整的渲染方程计算相对费时，常常消耗大量计算资源。在实践中常常使用简化渲染方程，这种方程在求解空间某点渲染方程时，并不考虑其它所有点对其影响，而只求解局部光照。大多数可视化系统均使用局部光照方法进行渲染。

高洛德着色（Gouraud）是法国计算机科学家Henri Gouraud发明的最常用的局部渲染算法。这种着色方法能够产生出很平滑的3D图形效果，它的原理是通过光照计算，计算出三角形三个顶点的颜色值，然后使用插值方法，对三角形中所有的像素进行插值计算，最后得到整个三角形的颜色值。Phong着色是美国科学家Phong Bui Tuong发明的另一种局部求解的算法。在高洛德算法中，每个三角形仅在顶点处有一个法向，而Phong算法对三角形内部每点的法向也做了插值操作，从而得到处理反射光（尤其是近点光源的反射光）时优于高洛德算法的表现。

如上图所示，左图为使用平面着色，即一个多边形上所有点使用同样渲染参数；中图为使用高洛德着色效果；右图为使用Phong着色效果。

 

蒙板渲染

渲染方程只能为多边形提供单一颜色，但现实生活中的对象往往具有大量细节特征，如崎岖表面、岩心、遥感图片等。单纯的渲染技术在传达这些细节方面的能力有限，这时需要使用蒙板映射，这在计算机可视化技术中处于重要位置。蒙板映射的处理过程如下：首先假定蒙板图片定义于二维坐标系[s, t]上，这时假定蒙板映射过程为函数T，该函数将把[s, t]空间中所有点映射到3D物体表面。

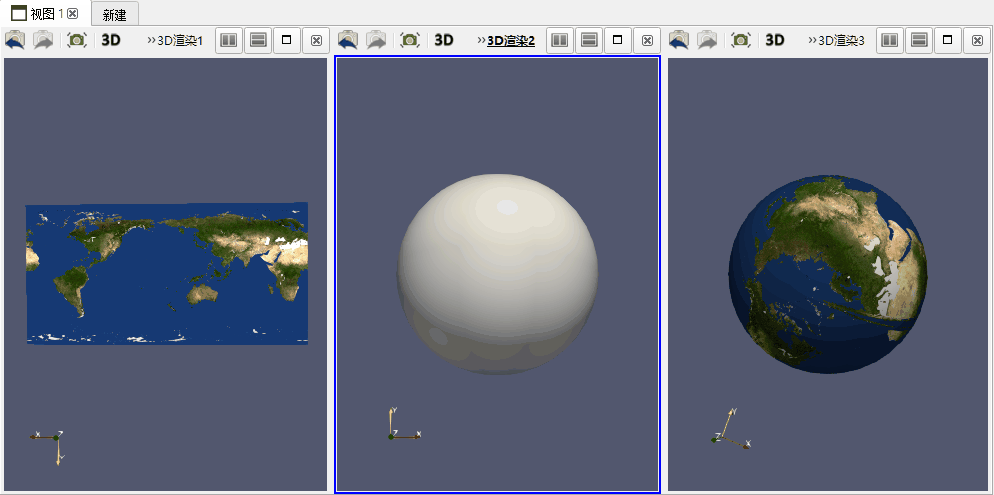
如上图所示，左图为蒙板材质图片，为长方形均匀网格数据结构，具有内在行列坐标[s,t]，若需将此图片蒙赋在中图中所示的球面（球面坐标[x,y]）上，需要使用球面蒙板工具对[s,t]空间和[x,y]空间进行一一映射，得到右图所示结果。