Shepards法

最简单的反距离加权法是“Shepard法”（Shepard，1968），具体所用方程如下所示：

其中n表示散点集数量，f i 表示散点指定函数值（如散点集值），w i 表示分配到每个散点的加权函数。加权函数的经典表达式为：

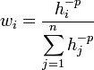
其中p表示加权指数，为一任意正实数，默认为2，可在使用经典加权函数选项中对加权指数进行修改。h i 表示散点和插值点之间的距离

其中 (x,y) 表示插值点坐标，(x i ,y i ) 表示散点坐标。加权函数随距散点距离的增加，由1（散点处）逐渐减小至零（远离散点）。加权函数为归一化函数，因此加权和为1。

上述加权函数是反距离加权插值的经典表达形式，在GMS中用到的是下述方程：

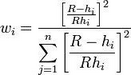
其中 h i 表示插值点与散点i之间的距离，R表示插值点与较远散点的距离，n表示散点总数量。此方程插值结果优于经典方程(Franke 和 Nielson, 1980)。

加权函数是一种欧几里得距离函数，每个散点的加权函数都径向对称。因此，所得插值面相对每个散点都有些对称，从而使得插值结果趋于散点的均值。Shepard法较简单，因此应用范围较广。

 

3D插值

Shepard法的3D方程与2D方程大致相同，不同的处在于距离计算公式的变化，具体如下所示：

其中 (x,y,z) 表示插值点坐标，(x i ,y i ,z i ) 表示每个散点的坐标。